{menu} {mirror}



The Countdown QuickPerm Algorithm (Head):
(Formally Example_01_Alpha)

QuickPerm - Head Permutations Using a Linear Array Without Recursion (Alpha) 

// NOTICE:  Copyright 1991-2008, Phillip Paul Fuchs

#define N    12   // number of elements to permute.  Let N > 2

void QuickPerm(void)
{
   unsigned int a[N], p[N+1];
   register unsigned int i, j, tmp; // Upper Index i; Lower Index j

   for(i = 0; i < N; i++)   // initialize arrays; a[N] can be any type
   {
      a[i] = i + 'A'; // a[i] value is not revealed and can be arbitrary
      p[i] = i;
   }
   p[N] = N; // p[N] > 0 controls iteration and the index boundary for i
   //display(a, 0, 0);   // remove comment to display array a[]
   i = 1;   // setup first swap points to be 1 and 0 respectively (i & j)
   while(i < N)
   {
      p[i]--;             // decrease index "weight" for i by one
      j = i % 2 * p[i];   // IF i is odd then j = p[i] otherwise j = 0
      tmp = a[j];         // swap(a[j], a[i])
      a[j] = a[i];
      a[i] = tmp;
      //display(a, j, i); // remove comment to display target array a[]
      i = 1;              // reset index i to 1 (assumed)
      while (!p[i])       // while (p[i] == 0)
      {
         p[i] = i;        // reset p[i] zero value
         i++;             // set new index value for i (increase by one)
      } // while(!p[i])
   } // while(i < N)
} // QuickPerm()
QuickPerm Function to Display Permutations (Optional) 

// NOTICE:  Copyright 1991-2008, Phillip Paul Fuchs

void display(unsigned int *a, unsigned int j, unsigned int i)            
{
   for(unsigned int x = 0; x < N; x++)
      printf("%c ",a[x]);
   printf("   swapped(%d, %d)\n", j, i);
   getch();  // press any key to continue...
} // display()
Fundamental Analysis of the QuickPerm Algorithm Above {Switch to Numbers}
Number of Objects
to Permute (N)		 a[N] Display of
Initial Sequence		 a[N] Display of
Final Sequence		 Total Number of Unique
Combinations Produced (N!)
3 A B C C B A                      {Output} 2 * 3 = 6
4 A B C D D A B C                   {Output} 6 * 4 = 24
5 A B C D E E B C D A                {Output} 24 * 5 = 120
6 A B C D E F F C D A B E 120 * 6 = 720
7 A B C D E F G G B C D E F A 720 * 7 = 5040
8 A B C D E F G H H C D E F A B G 5040 * 8 = 40320
9 A B C D E F G H I I B C D E F G H A 40320 * 9 = 362880
if N is even A B C . . . (N - 1) N N C D . . . (N - 2) A B (N - 1) (N - 1)! * N = N!
if N is odd A B C . . . (N - 1) N N B C . . . (N - 1) A (N - 1)! * N = N!


 A Permutation Ruler:
A Permutation Ruler


Tracking Lower Index
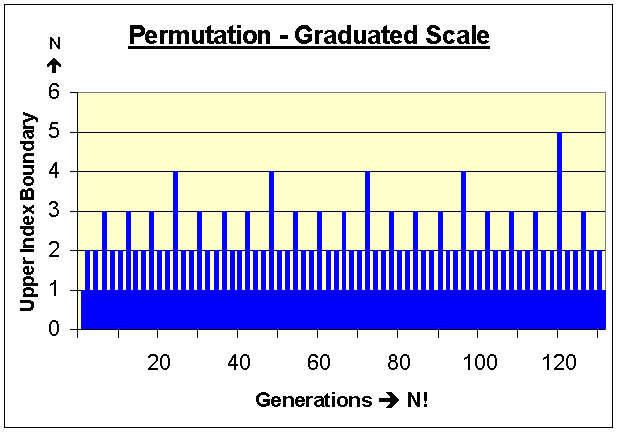
(Click here to enlarge graph.)


Next is tail permutations represented in EXAMPLE 02.